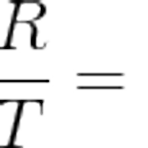 선형 회귀 분석의 결정계수를 통한 적합성 검증
선형 회귀 분석의 결정계수를 통한 적합성 검증
선형 회귀 분석에서 분석 데이터의 적합성 여부를 항상 고려해야 한다. 적합성 여부를 확인하는 방법 중 먼저 "결정계수(Coefficient of Determination, R-Square, R-제곱값, R2, R^2)"를 알아보자~ 결정계수는 "수식이 얼마나 X와 Y의 관계를 잘 표현하고 있는지" 나타내는 기준이다. 결정계수 (r-square) 일반적으로 결정계수는 0과 1사이의 값을 갖는데, 관계가 높을 수록 1에 가까운 값을 갖는다. 즉, 0에 가까워질수록, 수식에 데이터 분포를 제대로 표현하지 못하는 것이며, 1에 가까워지면 모든 데이터가 해당 수식에 접근한다는 것을 나타낸다. 결정계수를 나타내는 수식을 보면 다음과 같다. SSR, SST, SSE?? 처음 접할 경우, 용어를 모르기 때문에 어렵게 ..
 선형 회귀 분석의 데이터를 이해해 보자~
선형 회귀 분석의 데이터를 이해해 보자~
엑셀을 활용하여 선형 회귀 분석을 만드는 방법을 살펴봤다. 분산형 차트를 통해 선형 그래프를 그릴 수 있었다. 아래 그림을 보면, y= 0.002x - 0.6 이라는 수식이 보인다. 이것이 선형 회귀 분석에서 가장 필요로 하는 기본 수식이다. 선형 회귀 분석은 새로운 X 값이 주어졌을 때, Y 값을 예측하는 용도로 주로 사용한다. 위 예제는 "노출에 따른 클릭 수"로서 "만약 노출이 1500번 일어났다면, 클릭은 몇번 일어날까?" 같은 질문에 답을 줄 수 있다. 위 수식에서 x 대신 1500을 대입하면 된다. y = 0.002 x 1500 - 0.6 = 2.4 즉, 1500번 노출이 발생하면 2.4의 클릭이 일어날 것이라고 할 수 있다. 이런 수식을 선형 회귀 분석에서는 어떻게 구할까? "최소 자승법"이..
- Total
- Today
- Yesterday
- 도서
- 통계
- SCORM
- 마케팅
- 웹
- 맥
- 하둡
- 빅데이터
- fingra.ph
- HTML
- 프로젝트
- 분석
- 책
- 모바일
- 클라우드
- 디자인
- 구글
- 세미나
- 아이폰
- mysql
- ms
- 안드로이드
- XML
- 자바스크립트
- Hadoop
- 애플
- r
- java
- 자바
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
