 이산확률분포 #2 - 선형변환과 독립관측
이산확률분포 #2 - 선형변환과 독립관측
지난번에 이산확률분포에 대한 개념과 기대치, 분산을 구하는 방법에 대해서 정리해 봤습니다. 이어서 이산확률분포에서 사용할 수 있는 선형변환과 독립관측에 대해 살펴보기로 하겠습니다. 선형변환기대치를 구할 때 슬롯머신을 예로 들었는데요. 만약 슬롯머신이 게임당 1불에서 2불로 오르고. 당첨금도 5배가 올랐다고 생각해 보죠.. 이 경우, 기대치를 구하기 위해서는 각 수익에 대한 확률분포를 만들고 다음 공식을 사용하면 됩니다. 혹시 처음본다고 느끼시는 분은 이산확률분포#1 - 기대 수준을 관리 글을 다시 읽어 보시기 바랍니다. ^^ X를 Y로만 바꾼 겁니다. ㅠㅠ 그런데 우리는 이미 기존의 수익 X와 기대치 E(X), 그리고 분산 Var(X)까지 값을 알고 있습니다. 처음부터 하나씩 계산하지 않고 이런 정보를 ..
 이산확률분포 #1 - 기대 수준을 관리
이산확률분포 #1 - 기대 수준을 관리
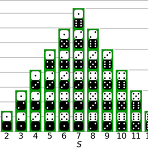
확률분포위키피디아에 따르면 확률분포를 다음과 같이 정의하고 있습니다.확률분포(probability distribution)는 확률변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다. 주사위를 던질거나 슬롯머신을 할 때 나올 수 있는 모든 가능성의 확률을 모아놓은 집합이 확률분포라고 할 수 있습니다. 다음 그림을 보면 주사위 두개를 던졌을 때 나올 수 있는 두 주사위의 합을 확률분포로 나타내고 있네요. 그러면 이를 수식으로는 어떻게 표현할까요? 정의를 다시 보면 "확률변수가 특정한 값을 가질 확률..." 이라고 되어 있습니다. 확률변수는 일반적으로 X나 Y와 같이 대문자로 표기합니다. 그리고 변수가 가질 수 있는 특정한 값은 x나 y처럼 소문자로 나타내죠.. 변수 X가 특정한 값 x를 가질 확률을 위..
 변이와 분포 - 분산과 표준편차
변이와 분포 - 분산과 표준편차
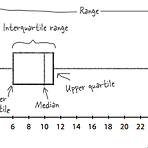
통계에서 분산이나 표준편차라는 말은 많이 들어봤고 수식도 외워봤지만 이것을 왜 써야 하는지는 모르고 배웠던 것 같습니다. 그래서 이번에는 분산과 표준편차를 중심으로 변이와 분포에 대해서 정리해 보려고 합니다. 범위앞서 평균과 관련해서 평균값, 중앙값, 최빈값을 정리했습니다. 만약 여러 사람의 데이터를 비교하려고 하는데 평균이 모두 동일한 경우라면, 데이터의 분포를 통해 비교해 볼 수 있을 것입니다. 데이터의 분포를 확인하는 가장 쉬운 방법은 바로 범위(range)입니다. 범위는 가장 큰 값에서 가장 작은 값을 빼면 되므로 쉽게 계산할 수 있습니다. 그러나 범위에서도 이상치가 나타나면 그 값의 폭이 너무 커지게 됩니다. 그래서 사분위수와 같은 것을 사용하기도 하는데요. 다음 그림(box and whiske..
