 R 예제: 데이터 세트에서 관계 확인하기
R 예제: 데이터 세트에서 관계 확인하기
R을 사용하면서 특정 파일에서 데이터를 읽어 분류하고 관계를 확인해야 하는 경우가 많이 있다. 이런 경우, 활용할 수 있는 간단한 예제를 살펴보도록 한다. (노만 매트로프의 빅데이터 분석 도구 R 프로그래밍 참조) 먼저 샘플로 사용할 아래 전복(abalone)의 데이터 파일을 다운로드 하자. 파일을 열어보면 다음과 같이 컴마(,)로 구분된 CSV 파일임을 알 수 있다. 여기에서 성별(Gender)에 따라 전복의 직경(Diameter)과 길이(Length)가 변화가 있는지 살펴보려고 한다. 전체 소스는 다음과 같다. read.csv 함수를 통해서 abalone.data 파일을 읽어들인다. 옵션을 살펴보면 헤더를 인식하도록 True값으로 설정했다. grps라는 빈 리스트 변수를 만들고 여기에 수컷과 암컷으로..
 몬테카를로 시뮬레이션~
몬테카를로 시뮬레이션~
분석을 하면서 "몬테카를로 시뮬레이션"을 한번쯤은 들어봤을 것이다. 몬테카를로는 무작위 값을 활용하여 확률적으로 계산하는 알고리즘을 이야기한다. 이렇게 확률적으로 계산함으로써 원하는 수치의 확률적 분포를 구할 수 있게 된다. 이를 위해 많은 수의 실험을 바탕으로 한 통계를 이용해 확률적 분포를 알게 되므로, 이것을 바로 몬테카를로 시뮬레이션이라고 한다. 몬테카를로 시뮬레이션 개념 몬테카를로는 통계 자료가 많고 입력값의 분포가 고를수록 정밀하게 시뮬레이션 할 수 있다. 그래서 컴퓨터를 이용해 시뮬레이션을 주로 한다. 또한 이론적 배경이나 복잡한 수식으로 계산해야 하는 경우, 근사치를 계산하기 위해서도 몬테카를로를 많이 사용한다. 몬테카를로 시뮬레이션은 모나코의 유명한 도박 도시이름을 따서 만들었다고 한다...
 다섯 번 왜?를 통한 문제 해결
다섯 번 왜?를 통한 문제 해결
에릭 리스는 린 스타트업에서 5번 왜라는 질문을 하면 문제의 본질에 도달할 수 있다고 했다. 5번 왜?라는 질문을 하는 것은 에릭 리스가 처음 주장한 것은 아니다. 이것은 오노 다이이치가 도요타에서 문제 해결을 위해 활용한 기법 중 하나이다. 생산 라인에서 문제가 발생하면 안돈 시스템(Andon System)이 가동되어 경고가 울리고 모든 라인이 정지된다. 이제 문제를 분석하고 해결해야 하는데, 이 때 5 Why를 이용해 문제의 근본을 해결하는 것이다. 즉, 5 Why는 근본적인 해결을 통해 문제의 재발을 방지하기 위한 도요타의 핵심 정신이다. 5 Why의 실제 사례를 보면 어떻게 문제의 근본에 접근해 가는지 알 수 있다. 트럭이 창고 앞에서 계속 대기해야 하는 문제가 발생했다. 빨리 지게차를 불러서 이..
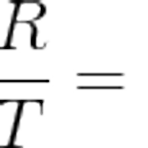 선형 회귀 분석의 결정계수를 통한 적합성 검증
선형 회귀 분석의 결정계수를 통한 적합성 검증
선형 회귀 분석에서 분석 데이터의 적합성 여부를 항상 고려해야 한다. 적합성 여부를 확인하는 방법 중 먼저 "결정계수(Coefficient of Determination, R-Square, R-제곱값, R2, R^2)"를 알아보자~ 결정계수는 "수식이 얼마나 X와 Y의 관계를 잘 표현하고 있는지" 나타내는 기준이다. 결정계수 (r-square) 일반적으로 결정계수는 0과 1사이의 값을 갖는데, 관계가 높을 수록 1에 가까운 값을 갖는다. 즉, 0에 가까워질수록, 수식에 데이터 분포를 제대로 표현하지 못하는 것이며, 1에 가까워지면 모든 데이터가 해당 수식에 접근한다는 것을 나타낸다. 결정계수를 나타내는 수식을 보면 다음과 같다. SSR, SST, SSE?? 처음 접할 경우, 용어를 모르기 때문에 어렵게 ..
 선형 회귀 분석의 데이터를 이해해 보자~
선형 회귀 분석의 데이터를 이해해 보자~
엑셀을 활용하여 선형 회귀 분석을 만드는 방법을 살펴봤다. 분산형 차트를 통해 선형 그래프를 그릴 수 있었다. 아래 그림을 보면, y= 0.002x - 0.6 이라는 수식이 보인다. 이것이 선형 회귀 분석에서 가장 필요로 하는 기본 수식이다. 선형 회귀 분석은 새로운 X 값이 주어졌을 때, Y 값을 예측하는 용도로 주로 사용한다. 위 예제는 "노출에 따른 클릭 수"로서 "만약 노출이 1500번 일어났다면, 클릭은 몇번 일어날까?" 같은 질문에 답을 줄 수 있다. 위 수식에서 x 대신 1500을 대입하면 된다. y = 0.002 x 1500 - 0.6 = 2.4 즉, 1500번 노출이 발생하면 2.4의 클릭이 일어날 것이라고 할 수 있다. 이런 수식을 선형 회귀 분석에서는 어떻게 구할까? "최소 자승법"이..
 엑셀을 활용한 회귀분석~
엑셀을 활용한 회귀분석~
엑셀은 장부 정리와 같은 기본적인 스타일시트 툴로 잘 알려져 있지만, 분석(Analysis) 측면에서도 정말 괜찮은 프로그램이다. 오늘은 엑셀을 이용해서 선형 회귀 분석을 수행하는 방법을 정리해 보려고 한다. 선형 회귀 분석(Linear Regression)… 말이 어려워 보일 뿐, 중고등학교 시절 수학 시간에 배운 X축, Y축의 선형 그래프를 생각해 보면 된다. 엑셀로 선형 회귀 분석을 하기 위해서 간단한 데이터를 만들어 보자. 광고 노출과 클릭간의 관계를 살펴볼 수 있는 데이터를 가상으로 구성한다. (다음 글에서 실제 광고 노출/클릭 데이터를 가지고 회귀분석을 해 볼 계획이다.) 다음과 같은 결과를 만드는 것이 최종 목표이다. 분산형 차트 활용 먼저 엑셀에서 출력할 위 데이터를 모두 선택한 후, "삽..
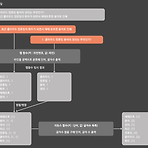 BigData 처리를 위한 맵리듀스(MapReduce)에 대하여~
BigData 처리를 위한 맵리듀스(MapReduce)에 대하여~
맵리듀스 개요 맵리듀스(MapReduce)는 기존 하드웨어를 활용한 분산 프로그래밍 모델로서, 대용량 데이터를 빠르고 안전하기 처리하기 위해 만들었다. 2014년 OSDI 컨퍼런스에서 구글이 "MapReduce : Simplified Data Processing on Large Clusters" 논문을 발표한 이후, 맵리듀스는 관심을 받기 시작했다. 그리고 오픈소스 루씬(Lucene)의 개발자인 더그 커팅(Doug Cutting)이 하둡(Hadoop)을 만들면서 맵리듀스가 널리 알려졌다. 하둡 오픈 소스 프로젝트는 구글의 분산 기술(GFS, MapReduce)을 기반으로 2006년부터 시작했다. 하둡 파일 시스템(HDFS)는 대규모 분산 파일 시스템 구축의 성능과 안전정을 보여줬고, 맵리듀스는 HDFS에..
 하둡(Hadoop) 관련 기술 - 피그, 주키퍼, HBase에 대한 간략한 정리!
하둡(Hadoop) 관련 기술 - 피그, 주키퍼, HBase에 대한 간략한 정리!
하둡과 관련해 HDFS(하둡 파일 시스템), MapReduce(맵리듀스)를 기본적으로 알아야 합니다. 그러나 때로는 하둡 에코 시스템으로 제공하는 도구들을 이해하면 좀 더 빠르고 쉽게 하둡 프로그래밍을 할 수 있습니다. 이번에는 하둡과 관련된 많은 프로젝트들 중에서 피그(pig), HBase, 주키퍼(Zookeeper)에 대해서 간략하게 개념을 정리하려고 합니다. 해당 개념들을 살펴보고 추후 필요할 때 활용하면 좋겠네요. 피그(Pig) 피그는 대용량 데이터셋을 좀 더 고차원적으로 처리할 수 있도록 합니다. 맵리듀스에서 처리할 수 없는 부분들을 지원한다고 하는데요. 대표적으로 조인(Join)과 같은 연산이 가능합니다. 피그는 다중 값과 중첩된 형태를 보이는 좀 더 다양한 데이터 구조를 지원하고, 데이터에 ..
 Hive & Pig - 하둡(Hadoop)의 맵리듀스를 보다 편하게~
Hive & Pig - 하둡(Hadoop)의 맵리듀스를 보다 편하게~
하둡(Hadoop) 프로젝트를 진행할 때 사람들의 고민이 무엇일까? 하고 생각해 봤습니다. Java 언어에 익숙하더라도 첫번째로 만나는 문제는 역시 맵리듀스(MapReduce)가 아닐까 합니다. 맵리듀스는 맵과 리듀스가 합쳐진 것으로 각각의 Map 함수와 Reduce 함수를 구현하고 JobClient를 통해 호출해야 합니다. 그런데 일반적으로 하둡 프로젝트에서 한번만 맵리듀스를 사용하는 경우는 거의 없습니다. 대부분 맵 리듀스를 반복적으로 사용하게 됩니다. 여기에 맵리듀스에서 기본적으로 사용하는 타입인 Text, IntWritable, LongWritable과 같은 것 이외에 객체를 사용한다든지. Key 항목이 아닌 Value에 속하는 항목으로 정렬을 하고 싶다든지, 하는 경우에 많은 개발자들이 어려움을..
 Cloudera Impala - 하둡 기반의 SQL 쿼리 엔진으로 실시간 분석을
Cloudera Impala - 하둡 기반의 SQL 쿼리 엔진으로 실시간 분석을
Cloudera Impala 소개 Cloudera Impala는 SQL 형태로 Hadoop의 데이터를 이용해 실시간으로 분석할 수 있는 시스템이다. 이것은 MapReduce 프레임워크를 사용할 때, 배치 처리로 인한 지연이 발생하는 것을 최적화 한 것이다. 구글에서도 2006년부터 기존의 GFS와 MapReduce에 실시간 처리가 가능한 Dremel을 본격적으로 활용하고 있다. Apache Hadoop의 HDFS와 MapReduce가 구글의 GFS, MapReduce 논문을 기반으로 만들어진 것처럼, Cloudera Impala도 2010년 발표된 구글의 Dremel 논문을 기반으로 하고 있다. 다만, SQL과 유사한 형태를 하둡에서 활용하기 위해 Hive의 쿼리 방식의 인터페이스를 가져왔다. 하둡을 C..
- Total
- Today
- Yesterday
- 도서
- 자바스크립트
- 클라우드
- 분석
- 책
- 아이폰
- java
- r
- fingra.ph
- 안드로이드
- 하둡
- XML
- 마케팅
- mysql
- SCORM
- 구글
- HTML
- 모바일
- ms
- 디자인
- 맥
- 프로젝트
- 세미나
- Hadoop
- 자바
- 통계
- 웹
- 빅데이터
- 애플
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
